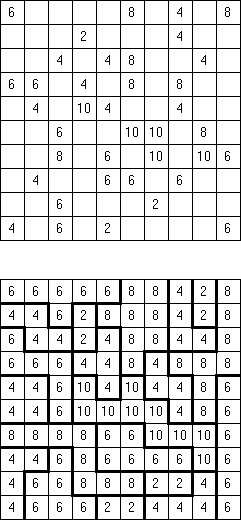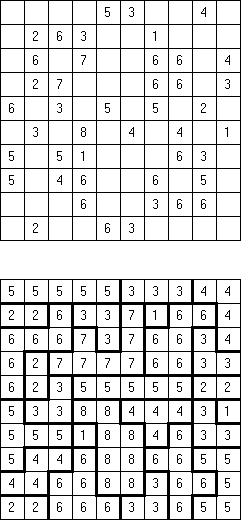
Fillomino ("Polyominous") is a type of logic puzzle. It is played on a rectangular grid of squares. Some cells of the grid start containing numbers, referred to as "givens". The goal is to divide the grid into blocks. The block must contain the number of cells indicated by the number in the cells of the block. The block cannot touch a similarly sized block, horizontally or vertically. Cells without numbers may form blocks necessary to complete the puzzle.

Cross+A can solve puzzles from 4 x 4 to 40 x 40.
There are many variations of Fillomino puzzle. Some of them can be solved by Cross+A.
No Rectangles Fillomino: rectangular regions are not allowed.
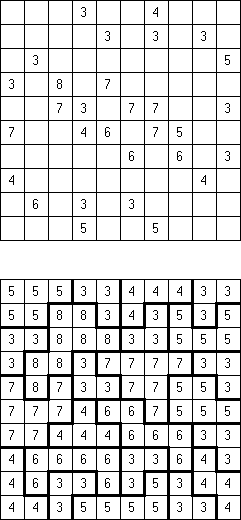
Only Rectangles Fillomino: all regions must be rectangular.
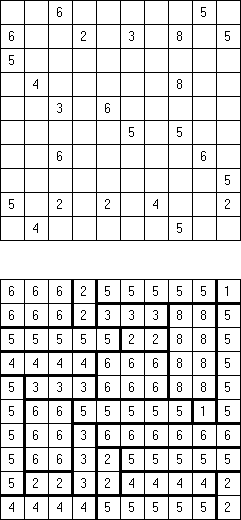
No 2 x 2 Squares Fillomino: no 2 x 2 cell area within the grid can contain the same numbers.
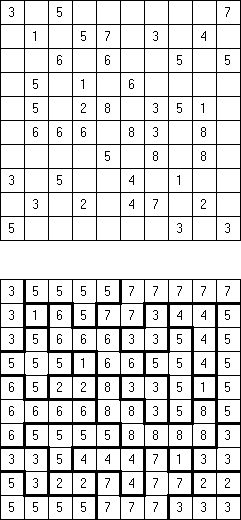
Non-Consecutive Fillomino: any two adjacent regions must differ in size by at least two.
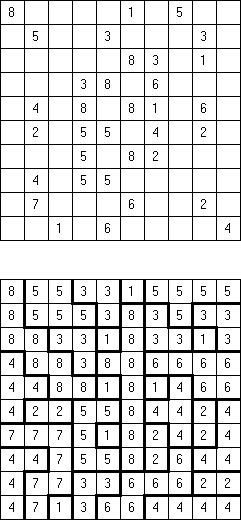
Consecutive Fillomino: any region of size N must be orthogonally adjacent to at least one other region of size N-1 or N+1.
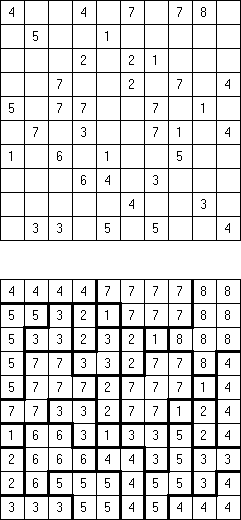
No Row/Column Repeats Fillomino: in each row and each column all cells with the same number must belong to the same region.
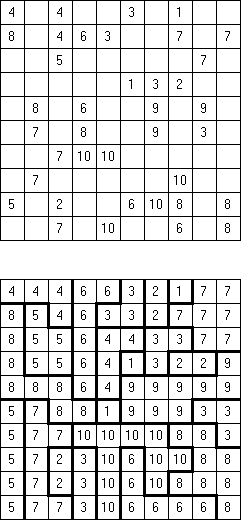
All Odds Fillomino: the size of each region must be an odd number.
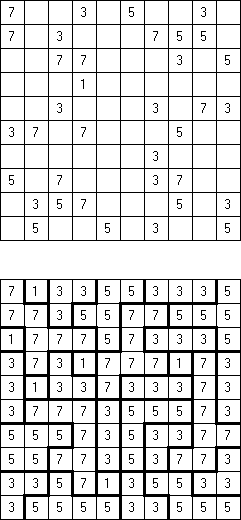
All Evens Fillomino: the size of each region must be an even number.